Decomposition

• There are various regimes for signal decomposition.

• Examples:

  • Fast Fourier Transform (FFT)

  • Wavelets

  • Linear components

• Motviation:

  • Trend discovery

  • Low-pass/high-pass filter

  • Exploratory data analysis

Fast Fourier Transform

FFT history and application

• An important workhorse in signal processing.

• Can be traced back to Carl Friedrich Gauss on Discrete Fourier Transforms from 1805.

• Major milestone in 1965 by James Cooley and John Tukey regarding speed of computations and applications in detecting Soviet nuclear bomb tests.

• Used in anything from mathematical speed-ups, via video and music compression, modern signal processing in Wi-Fi, 5G, etc. to finance.

FFT function

• Wikipedia: A Fourier Transform is a transform that converts a function into a form that describes the frequencies present in the original function.

• scipy.fft: Fourier analysis is a method for expressing a function as a sum of periodic components, and for recovering the signal from those components.

\[X_k = \sum_{n=0}^{N-1} x_n e^{i2 \pi kn/N} ~~~~ k = 0, ..., N-1\]

• Here, k is the index of a signal, X, and N is its length. \(x_n\) is a coefficient to be fitted.

import numpy as np
import matplotlib.pyplot as plt
N = 100
n = 1
x = [np.exp(1j * 2 * np.pi * k * n / N) for k in range(N)]
plt.plot(range(N), np.real(x), '.')
plt.ylabel('Real part')
plt.show()

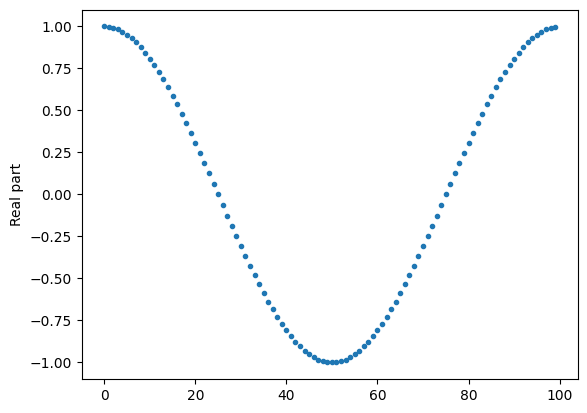
# The full complex exponential basis
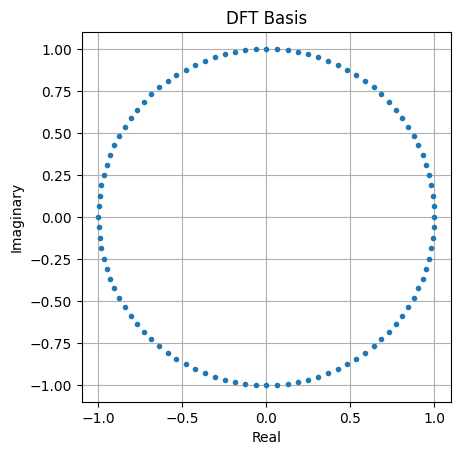
plt.plot(np.real(x), np.imag(x), '.')
plt.axis('square')
plt.grid()
plt.xlabel('Real')
plt.ylabel('Imaginary')
plt.title('DFT Basis')
plt.show()

Direct Cosine Transform (DCT)

• FFT with real valued data.

• For real numbered signals, the definition above can be exchanged with a version based on the cosine or sine functions.

• There are theoretically 8+8 “types”, 4+4 of which are implemented in SciPy, and various choices for normalisation.

• Type I DCT (Direct Cosine Transform) as implemented in SciPy:

\[y_k = x_0 + (-1)^k x_{N-1} + 2 \sum_{n=1}^{N-2} x_n cos (\frac{\pi k n}{N-1}))\]

• \(y_k\) is the \(k\)-th part of the signal, \(N\) is the length, \(x_n\) is the \(n\)-th coefficient.

• Coefficient signs indicate flip of the base cosines, magnitudes indicate scaling.

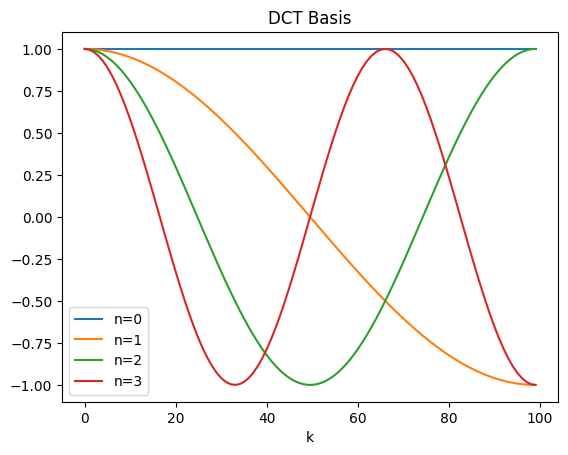
• n indicates the number of half cosine cycles, i.e., even n means full cycles (see plot below), maximum frequency of n/2.

• Quicker than FFT and guarantees real valued frequency domain.

N = 100
n = 3
for k in range(0,n+1):
    plt.plot(np.cos(np.pi*k*np.arange(N)/(N-1)), label='n='+str(k))
plt.title('DCT Basis')
plt.xlabel('k')
plt.legend()
plt.show()

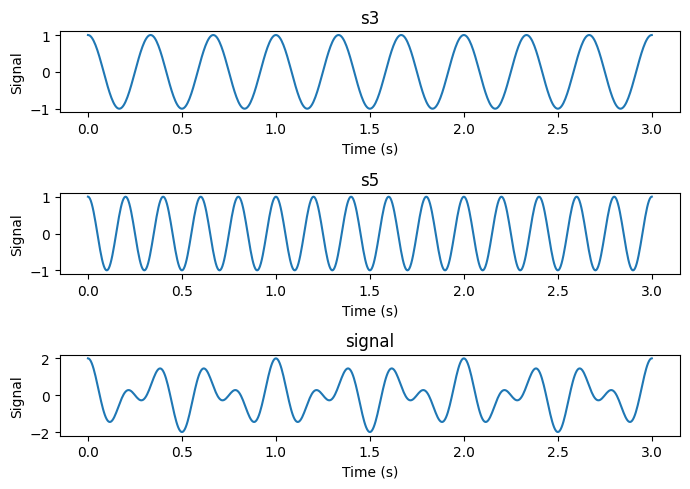
# Sum of two cosines with different frequencies.
import numpy as np
from scipy.fft import dct, idct

N = 601
s = 3
time = np.linspace(0,s,N)
s3 = np.cos(3 * 2*np.pi * time)
s5 = np.cos(5 * 2*np.pi * time)
signal = s3 + s5

# Make three suplots above each other with s3, s5 and signal
fig, axs = plt.subplots(3, 1, figsize=(7, 5))
axs[0].plot(time, s3)
axs[0].set_title('s3')
axs[1].plot(time, s5)
axs[1].set_title('s5')
axs[2].plot(time, signal)
axs[2].set_title('signal')
for ax in axs.flat:
    ax.set(xlabel='Time (s)', ylabel='Signal')
plt.tight_layout()
plt.show()

# Print the resolution of the time axis in Hz
dt = time[1] - time[0]
print('Sampling of the time axis:', 1/dt, 'Hz')

Sampling of the time axis: 200.0 Hz

# Discrete Cosine transform
shift = 0 # Shift the signal to the right by this amount, e.g., 100
fourier_signal = dct(np.concatenate([np.zeros(shift),signal]), type=1, norm="forward") # Pad with zeros to shift signal
dt = time[1] - time[0]
W = np.linspace(0, 1/(2*dt), N+shift)
#                    ^-- Frequency axis in Hz (2* because of of definitions of DCT with half integers)

# Plot the Fourier transform
fig, axs = plt.subplots(2, 1, figsize=(7, 4))
axs[0].plot(range(N+shift), fourier_signal)
axs[0].set_xlabel('Coefficient')
axs[0].set_ylabel('Fourier Transform')
axs[0].set_xlim(0, N+shift)
axs[1].plot(W, fourier_signal)
axs[1].set_xlabel('Frequency (Hz)')
axs[1].set_ylabel('Fourier Transform')
axs[1].set_xlim(0, np.max(W))
plt.tight_layout()
plt.show()

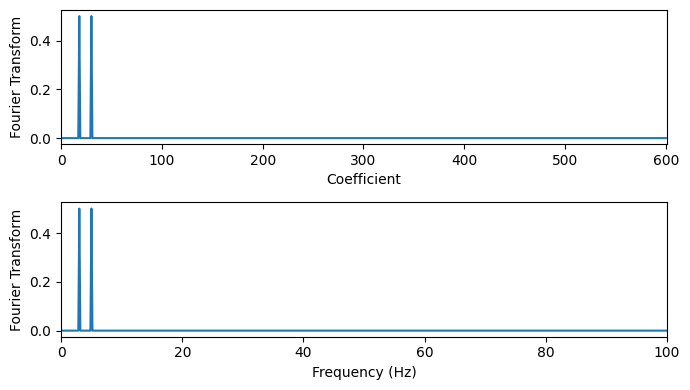
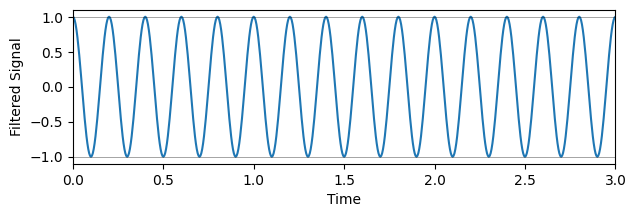
FFT filtering

• We can apply the FFT to analyse the frequencies present or to filter the signal.

  • Filtering here means that some frequencies are removed from the signal.

• Typical filters are:

  • Low-pass filter: Remove high frequencies, e.g., noise or short-term changes, focusing on trends or slowly changing signals.

  • High-pass filter: Remove low frequencies, e.g., trends or baselines, focusing on rapid changes or anomalies.

plt.plot(W)
plt.show()

# Remove frequencies below 4, i.e., a high-pass filter
filtered_fourier_signal = fourier_signal.copy()
filtered_fourier_signal[(W<4)] = 0 # <- Come playe with me!
cut_signal = idct(filtered_fourier_signal, type=1, norm="forward")

# Plot the filtered signal
plt.figure(figsize=(7,2))
plt.plot(time, cut_signal)
plt.xlabel('Time')
plt.ylabel('Filtered Signal')
plt.xlim(0,s)
plt.axhline(-1, color='k', alpha=0.5, linewidth=0.5) # Shows the inexactness of the reconstruction
plt.axhline(1, color='k', alpha=0.5, linewidth=0.5)
plt.show()

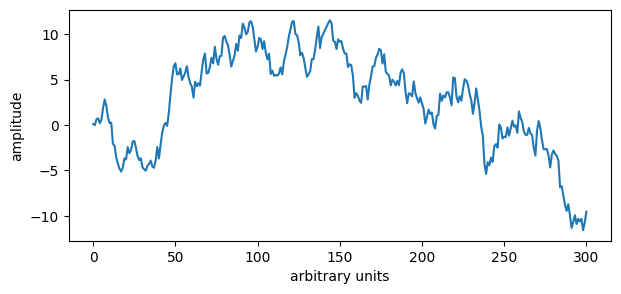
# A curve we have seen before
N = 301
rng = np.random.default_rng(0)
y = rng.standard_normal(N).cumsum()

# Plot the curve
plt.figure(figsize=(7,3))
plt.plot(y)
plt.xlabel('arbitrary units')
plt.ylabel('amplitude')
plt.show()

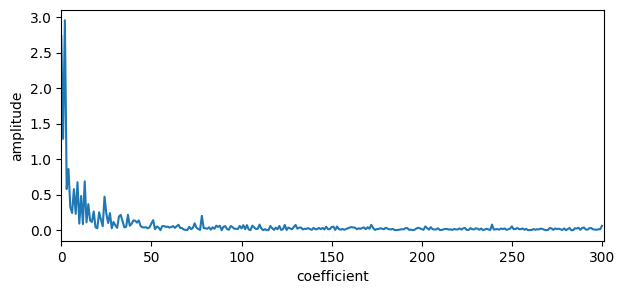
# Plot the Fourier transform
plt.figure(figsize=(7,3))
plt.plot(np.abs(dct(y, type=1, norm="forward"))) # Not caring about the signs
#plt.plot(dct(y, type=1)) # Caring about the signs
plt.xlabel('coefficient')  # Think 1/width of time series
plt.ylabel('amplitude')
plt.xlim(0,N)
plt.show()

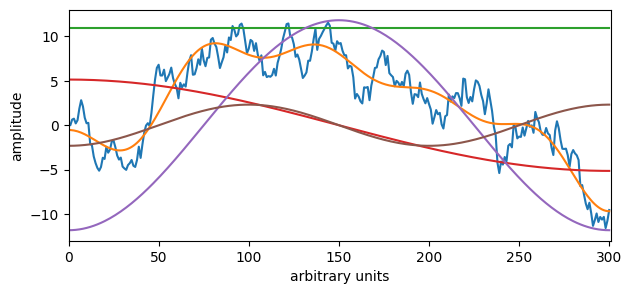
Overlay cosines on signal

# Remove frequencies above 50, i.e., a low-pass filter.
W = np.arange(0, N) # Frequency axis
filtered_fourier_signal = dct(y, type=1, norm="forward")
x = filtered_fourier_signal.copy()
filtered_fourier_signal[(W > 10)] = 0
cut_signal = idct(filtered_fourier_signal, type=1, norm="forward")
add_cosines = 3 # <- Change me! Non-negative number adds cosines to the filtered signal

# Plot the filtered signal
plt.figure(figsize=(7,3))
plt.plot(y)
plt.plot(cut_signal)
plt.xlabel('arbitrary units')
plt.ylabel('amplitude')
plt.xlim(0,N)
if add_cosines > -1:
    for k in range(0,add_cosines+1):
        plt.plot(2 * x[k] * np.cos(np.pi*k*np.arange(N)/(N-1)) * 2) # Scaled up by 2 to fit in plot
plt.show()
#print('Sum of original signal: {:.2f}'.format(np.sum(y)))
#print('0th DCT coefficient / 2: {:.2f}'.format(filtered_fourier_signal[0]/2)) # Only holds for type 2 DCT with norm="backward"

\[y_k = x_0 + (-1)^k x_{N-1} + 2 \sum_{n=1}^{N-2} x_n cos (\frac{\pi k n}{N-1}))\]

Linear decomposition

• Various forms of linear models can be used for decomposition, each having different focus or optimality criteria, e.g.:

  • Seasonal-Trend decomposition using LOESS in the statmodels package

  • Multivariate explorative data analysis with Principal Component Analysis.

Seasonal-Trend decomposition using LOESS (STL)

• STL takes a (time) series as input together with an estimate of period length.

• Output are:

  • A trend along the series (T).

  • A seasonal signal which may evolve along the series (S).

  • A residual ®.

  • Additive: X = T + S + R

  • (Multiplicative: X = T * S * R)

• Additional parameters:

  • Length of smoothers for trend and season (high number = less change).

  • Use weighting of samples for robustness (allow more individual deviation from trend/season).

Fitting:

• Typically STL is fitted one component at a time.

  • Smooth the series to estimate the trend,
    \(T = f_{smooth,T}(X)\).

  • Subtract the trend from the series,
    \(X_{S+R} = X - T\).

  • Average across seasons with sliding window (LOESS) to estimate the season,
    \(S = f_{smooth,S}(X_{S+R})\).

  • Subtract the trend and season from the signal to estimate the residual,
    \(R = X - T - S\)

# Monthly sunspots from https://github.com/jbrownlee/Datasets

# Load the data
import pandas as pd
sunspots = pd.read_csv("../../data/monthly-sunspots.csv", header=0)
print(sunspots.shape)
sunspots.head()

(2820, 2)

	Month	Sunspots
0	1749-01	58.0
1	1749-02	62.6
2	1749-03	70.0
3	1749-04	55.7
4	1749-05	85.0

# Plot the data
sunspots.plot.line(x='Month', y='Sunspots', figsize=(7,2))
plt.xlabel('Month')
plt.ylabel('Number of sunspots')
plt.show()

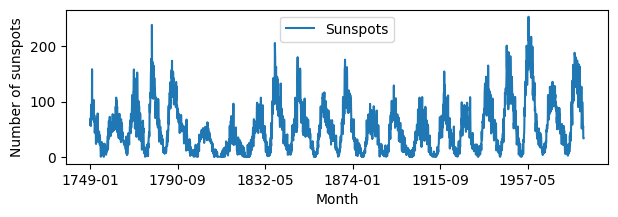
# Approximate periodicity: Lenght of series divided by number of periods.
# For sunspots we know that there is a periodicity of approximately 11 years.
np.round(2820/21)

np.float64(134.0)

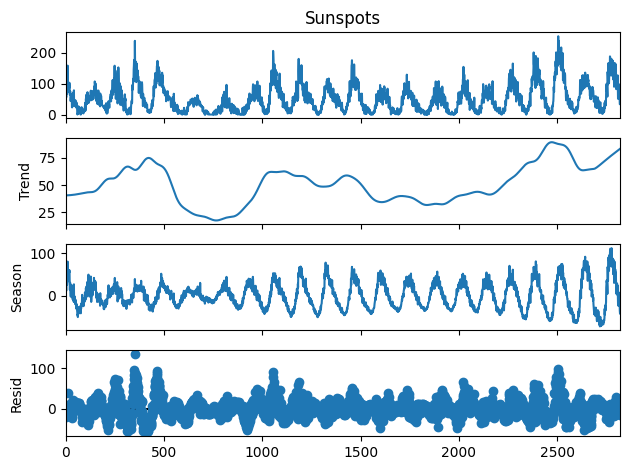
from statsmodels.tsa.seasonal import STL
stl = STL(sunspots["Sunspots"], period=134)#, robust=True, seasonal=141, trend=141)
res = stl.fit() # Contains the components and a plot function
fig = res.plot()

# Daily Female Births in California from https://github.com/jbrownlee/Datasets

# Load the data
births = pd.read_csv("../../data/daily-total-female-births.csv", header=0)
births.head()

	Date	Births
0	1959-01-01	35
1	1959-01-02	32
2	1959-01-03	30
3	1959-01-04	31
4	1959-01-05	44

stl = STL(births["Births"], period=7)
res = stl.fit()
fig = res.plot()

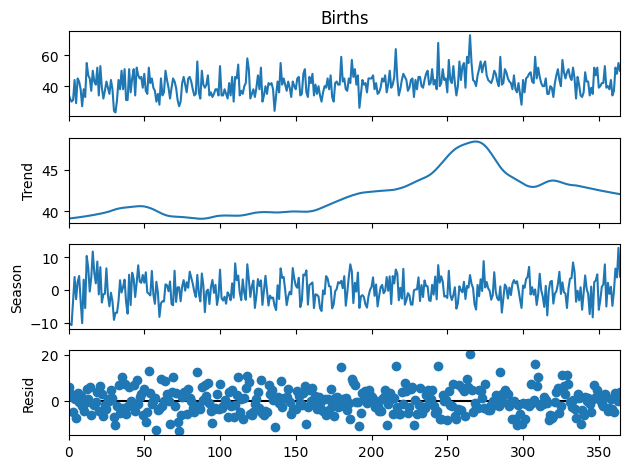
Excercise

• Force the period to change less.

• Extract the trend and plot it as a function of time.

• Indicate the date of maximum number of conceptions (~9 months before birth), assuming the year is cyclic.

Multiple seasonalities

• If a there is more than one phenomenon with a cyclic behaviour, multiple seasonalities can be found through Multiple Seasonal-Trend decomposition using LOESS (MSTL).

• The more complex model one applies, the higher the chances of overfitting!

• Example at statsmodels.org

Principal Component Analysis (PCA)

• For (time) series with multiple variables, PCA can give a first indication of structure and connection between variables.

• Scores show paths of time points, loadings show how variables relate.

• One PCA formulation for input data \(\mathbf{X}\) with series as columns:

\[\mathbf{U} \mathbf{S} \mathbf{V}' = svd(\mathbf{X}-\bar{\mathbf{X}})\]

\[\mathbf{T} = \mathbf{U} \mathbf{S} \text{ - scores}\]

\[\mathbf{P} = \mathbf{V}' \text{ - loadings}\]

Beijing pollution data

This dataset is originally from UCI Machine Learning Repository and shows hourly measurements of weather at the US embassy in Bejing. Its columns are:

1. No: row number

2. year: year of data in this row

3. month: month of data in this row

4. day: day of data in this row

5. hour: hour of data in this row

6. pm2.5: PM2.5 concentration (\(\mu g/m^3\))

7. DEWP: Dew Point (\(^{\circ}F\))

8. TEMP: Temperature (\(^{\circ}F\))

9. PRES: Pressure (hPa)

10. cbwd: Combined wind direction

11. Iws: Cumulated wind speed

12. Is: Cumulated hours of snow

13. Ir: Cumulated hours of rain

# Beijing pollution data from https://github.com/jbrownlee/Datasets

# Load the data
pollution = pd.read_csv("../../data/pollution.csv", header=0, index_col=0)
print(pollution.shape)
pollution.head()

(43824, 12)

	year	month	day	hour	pm2.5	DEWP	TEMP	PRES	cbwd	Iws	Is	Ir
No
1	2010	1	1	0	NaN	-21	-11.0	1021.0	NW	1.79	0	0
2	2010	1	1	1	NaN	-21	-12.0	1020.0	NW	4.92	0	0
3	2010	1	1	2	NaN	-21	-11.0	1019.0	NW	6.71	0	0
4	2010	1	1	3	NaN	-21	-14.0	1019.0	NW	9.84	0	0
5	2010	1	1	4	NaN	-20	-12.0	1018.0	NW	12.97	0	0

# Recode the cbwd column using one-hot encoding and add to the data frame
pollution = pd.concat([pollution, pd.get_dummies(pollution["cbwd"], dtype=float)], axis=1)
pollution = pollution.drop(columns=["cbwd"])
pollution.head()

	year	month	day	hour	pm2.5	DEWP	TEMP	PRES	Iws	Is	Ir	NE	NW	SE	cv
No
1	2010	1	1	0	NaN	-21	-11.0	1021.0	1.79	0	0	0.0	1.0	0.0	0.0
2	2010	1	1	1	NaN	-21	-12.0	1020.0	4.92	0	0	0.0	1.0	0.0	0.0
3	2010	1	1	2	NaN	-21	-11.0	1019.0	6.71	0	0	0.0	1.0	0.0	0.0
4	2010	1	1	3	NaN	-21	-14.0	1019.0	9.84	0	0	0.0	1.0	0.0	0.0
5	2010	1	1	4	NaN	-20	-12.0	1018.0	12.97	0	0	0.0	1.0	0.0	0.0

# Replace NaN with 0 in the pm2.5 column
pollution["pm2.5"] = pollution["pm2.5"].fillna(0)
pollution.head()

	year	month	day	hour	pm2.5	DEWP	TEMP	PRES	Iws	Is	Ir	NE	NW	SE	cv
No
1	2010	1	1	0	0.0	-21	-11.0	1021.0	1.79	0	0	0.0	1.0	0.0	0.0
2	2010	1	1	1	0.0	-21	-12.0	1020.0	4.92	0	0	0.0	1.0	0.0	0.0
3	2010	1	1	2	0.0	-21	-11.0	1019.0	6.71	0	0	0.0	1.0	0.0	0.0
4	2010	1	1	3	0.0	-21	-14.0	1019.0	9.84	0	0	0.0	1.0	0.0	0.0
5	2010	1	1	4	0.0	-20	-12.0	1018.0	12.97	0	0	0.0	1.0	0.0	0.0

# PCA of pollution data
from hoggorm.pca import nipalsPCA as PCA
pca = PCA(pollution.iloc[:,4:].values, numComp=4, Xstand=True)

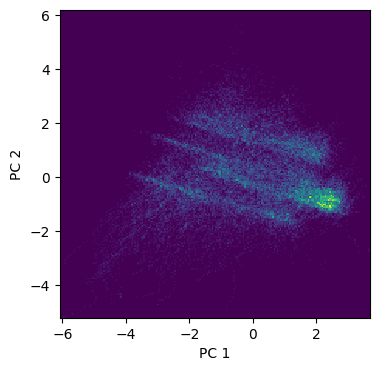
# Make a 2D histogram of the X_scores (too many points for a scatter plot)
plt.figure(figsize=(4,4))
plt.hist2d(pca.X_scores()[:,0], pca.X_scores()[:,1], bins=200)
plt.xlabel("PC 1")
plt.ylabel("PC 2")
plt.show()

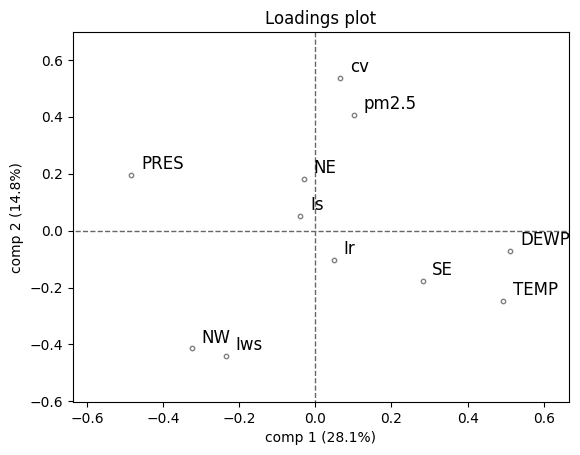
# Loading plot
from hoggormplot import loadings
loadings(pca, comp=[1,2], XvarNames=pollution.columns[4:].tolist())
plt.show()

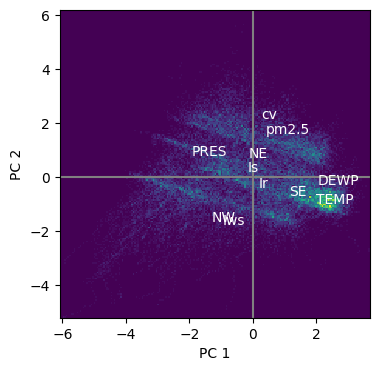
# Make a 2D histogram of the X_scores (too many points for a scatter plot)
plt.figure(figsize=(4,4))
plt.hist2d(pca.X_scores()[:,0], pca.X_scores()[:,1], bins=200)
plt.xlabel("PC 1")
plt.ylabel("PC 2")
labs = pollution.columns[4:].tolist()
# Add an axis cross in gray using axhline and axvline
plt.axhline(0, color="gray")
plt.axvline(0, color="gray")
# Add the loadings as text (labs) in white on top of the histogram, scale to the same range as the histogram
for i in range(len(labs)):
    plt.text(pca.X_loadings()[i,0]*4, pca.X_loadings()[i,1]*4, labs[i], color="white")
plt.show()

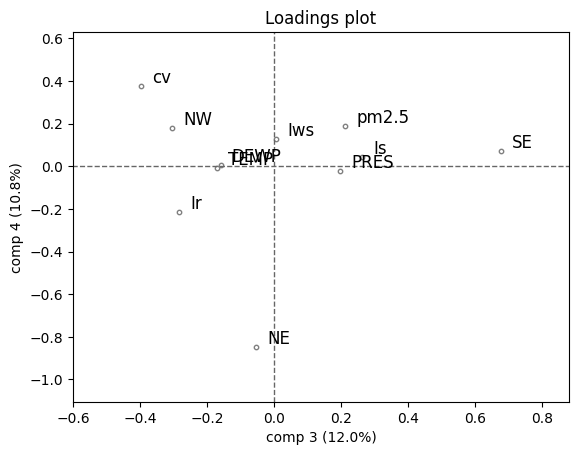
# Plot the 3rd and 4th components
loadings(pca, comp=[3,4], XvarNames=pollution.columns[4:].tolist())
plt.show()

See also

Resources

• Wikipedia: Fast Fourier Transform

• Wikipedia: Discrete Cosine Transform

• SciPy: Fourier Transforms

• Seasonal-Trend decomposition using LOESS

• YouTube: Veritasium - the history of FFT (26m:33s)