L-PLS regression

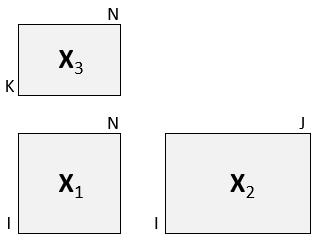
Simultaneous decomposition of three blocks connected in an L pattern.

lpls(
  X1,
  X2,
  X3,
  ncomp = 2,
  doublecenter = TRUE,
  scale = c(FALSE, FALSE, FALSE),
  type = c("exo"),
  impute = FALSE,
  niter = 25,
  subsetX2 = NULL,
  subsetX3 = NULL,
  ...
)

Arguments

X1

matrix of size IxN (middle matrix)

X2

matrix of size IxJ (left matrix)

X3

matrix of size KxN (top matrix)

ncomp

number of L-PLS components

doublecenter

logical indicating if centering should be done both ways for X1 (default=TRUE)

scale

logical vector of length three indicating if each of the matrices should be autoscaled.

type

character indicating type of L-PLS ("exo"=default, "exo_ort" or "endo")

impute

logical indicating if SVD-based imputation of missing data is required.

niter

numeric giving number of iterations in component extraction loop.

subsetX2

vector defining optional sub-setting of X2 data.

subsetX3

vector defining optional sub-setting of X3 data.

...

Additional arguments, not used.

Value

An object of type lpls and multiblock containing all results from the L-PLS analysis. The object type lpls is associated with functions for correlation loading plots, prediction and cross-validation. The type multiblock is associated with the default functions for result presentation (multiblock_results) and plotting (multiblock_plots).

Details

Two versions of L-PLS are available: exo- and endo-L-PLS which assume an outward or inward relationship between the main block X1 and the two other blocks X2 and X3.

The exo_ort algorithm returns orthogonal scores and should be chosen for visual exploration in correlation loading plots. If exo-L-PLS with prediction is the main purpose of the model then the non-orthogonal exo type L-PLS should be chosen for which the predict function has prediction implemented.

References

• Martens, H., Anderssen, E., Flatberg, A.,Gidskehaug, L.H., Høy, M., Westad, F.,Thybo, A., and Martens, M. (2005). Regression of a data matrix on descriptors of both its rows and of its columns via latent variables: L-PLSR. Computational Statistics & Data Analysis, 48(1), 103 – 123.

• Sæbø, S., Almøy, T., Flatberg, A., Aastveit, A.H., and Martens, H. (2008). LPLS-regression: a method for prediction and classification under the influence of background information on predictor variables. Chemometrics and Intelligent Laboratory Systems, 91, 121–132.

• Sæbø, S., Martens, M. and Martens H. (2010) Three-block data modeling by endo- and exo-LPLS regression. In Handbook of Partial Least Squares: Concepts, Methods and Applications. Esposito Vinzi, V.; Chin, W.W.; Henseler, J.; Wang, H. (Eds.). Springer.

See also

Overviews of available methods, multiblock, and methods organised by main structure: basic, unsupervised, asca, supervised and complex. Functions for computation and extraction of results and plotting are found in lpls_results.

Author

Solve Sæbø (adapted by Kristian Hovde Liland)

Examples

# Simulate data set
sim <- lplsData(I = 30, N = 20, J = 5, K = 6, ncomp = 2)
X1  <- sim$X1; X2 <- sim$X2; X3 <- sim$X3
lp  <- lpls(X1,X2,X3) # exo-L-PLS