Sijmen de Jong's SIMPLS

Fits a PLSR model with the SIMPLS algorithm.

Usage

simpls.fit(
  X,
  Y,
  ncomp,
  center = TRUE,
  orthScores = FALSE,
  stripped = FALSE,
  ...
)

Arguments

X: a matrix of observations. NAs and Infs are not allowed.
Y: a vector or matrix of responses. NAs and Infs are not allowed.
ncomp: the number of components to be used in the modelling.
center: logical, determines if the \(X\) and \(Y\) matrices are mean centered or not. Default is to perform mean centering.
orthScores: logical. If TRUE the scores are orthogonalised for increased numerical precision (default = FALSE, for speed).
stripped: logical. If TRUE the calculations are stripped as much as possible for speed; this is meant for use with cross-validation or simulations when only the coefficients are needed. Defaults to FALSE.
...: other arguments. Currently ignored.

Value

A list containing the following components is returned:

coefficients: an array of regression coefficients for 1, ..., ncomp components. The dimensions of coefficients are c(nvar, npred, ncomp) with nvar the number of X variables and npred the number of variables to be predicted in Y.
scores: a matrix of scores.
loadings: a matrix of loadings.
Yscores: a matrix of Y-scores.
Yloadings: a matrix of Y-loadings.
projection: the projection matrix used to convert X to scores.
Xmeans: a vector of means of the X variables.
Ymeans: a vector of means of the Y variables.
fitted.values: an array of fitted values. The dimensions of fitted.values are c(nobj, npred, ncomp) with nobj the number samples and npred the number of Y variables.
residuals: an array of regression residuals. It has the same dimensions as fitted.values.
Xvar: a vector with the amount of X-variance explained by each component.
Xtotvar: Total variance in X.

If stripped is TRUE, only the components coefficients, Xmeans and Ymeans are returned.

Details

This function should not be called directly, but through the generic functions plsr or mvr with the argument method="simpls". SIMPLS is much faster than the NIPALS algorithm, especially when the number of X variables increases, but gives slightly different results in the case of multivariate Y. SIMPLS truly maximises the covariance criterion. According to de Jong, the standard PLS2 algorithms lie closer to ordinary least-squares regression where a precise fit is sought; SIMPLS lies closer to PCR with stable predictions.

References

de Jong, S. (1993) SIMPLS: an alternative approach to partial least squares regression. Chemometrics and Intelligent Laboratory Systems, 18, 251–263.

Author

Ron Wehrens and Bjørn-Helge Mevik

Examples

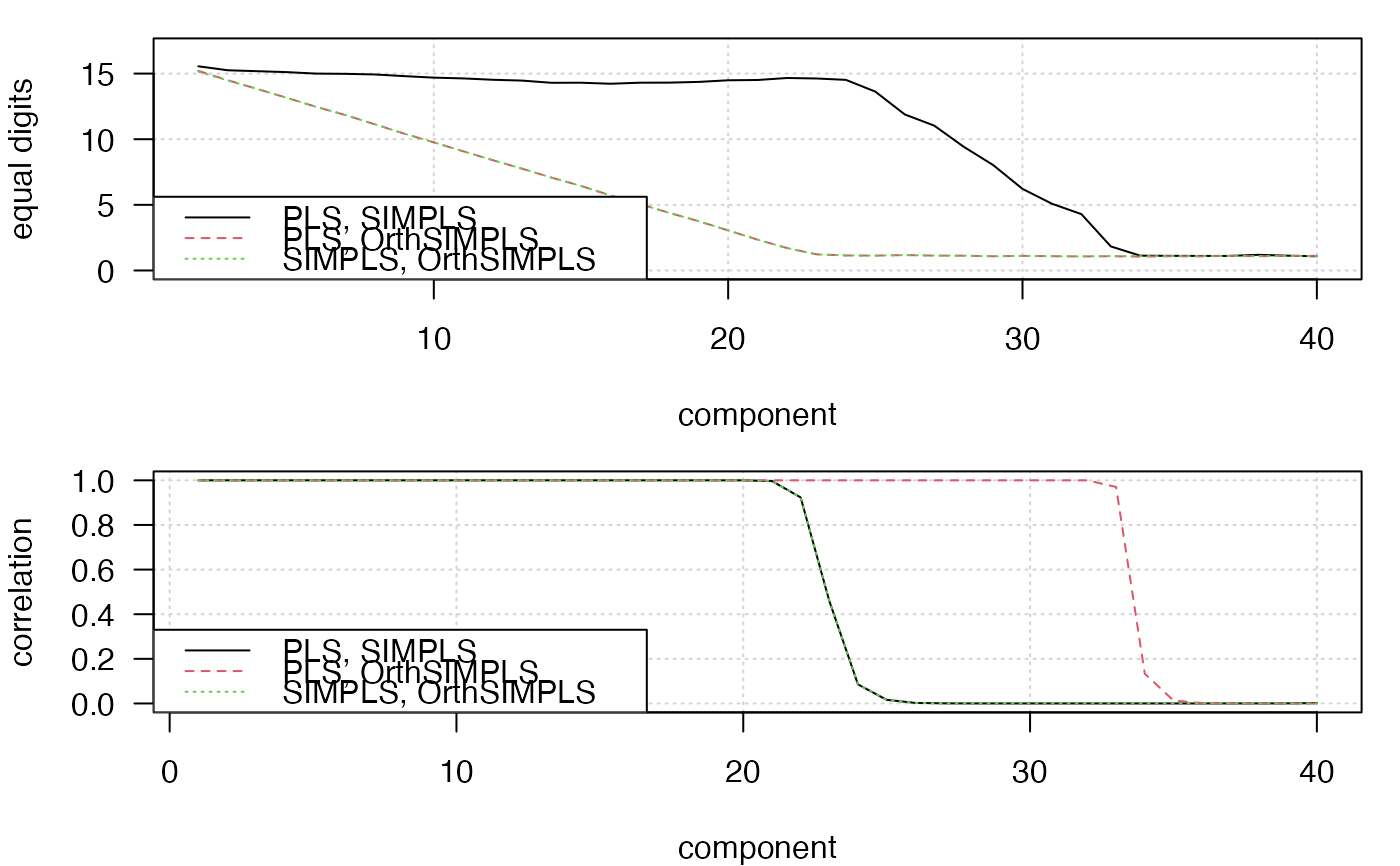
## Simulation of SIMPLS stability
# The graphics produced, demonstrate the numeric instability of the original
# SIMPLS without score orthogonalization.
set.seed(42)
N <- 100
p <- 2000
ncomp <- 40
simData <- data.frame(X = I(matrix(rnorm(N*p),N)), y = rnorm(N))
pls    <- plsr(y ~ X, data=simData, ncomp=ncomp)
simps  <- plsr(y ~ X, data=simData, ncomp=ncomp, method="simpls")
simpsO <- plsr(y ~ X, data=simData, ncomp=ncomp, method="simpls", orthScores=TRUE)
normScores <- pls$scores
for(i in 1:ncomp)
  normScores[,i] <- normScores[,i]/sqrt(sum(normScores[,i]^2))

# Check number of equal digits
eqDig <- function(x,y){
  xy <- abs(x - y)
  xy[xy == 0] <- 10^-16
  -colMeans(log10(xy))
}
eqDig_PLS_oSIMPLS    <- eqDig(normScores, simpsO$scores)
eqDig_SIMPLS_PLS     <- eqDig(simps$scores, normScores)
eqDig_SIMPLS_oSIMPLS <- eqDig(simps$scores, simpsO$scores)
# Correlation between models
cor_PLS_oSIMPLS    <- diag(cor(pls$scores,simps$scores))
cor_SIMPLS_oSIMPLS <- diag(cor(pls$scores,simpsO$scores))
cor_SIMPLS_PLS     <- diag(cor(simps$scores,simpsO$scores))

par.old <- par(mfrow=c(2,1), mar=c(4,4,1,1), las=1)
matplot(2:ncomp,cbind(eqDig_PLS_oSIMPLS,eqDig_SIMPLS_PLS, eqDig_SIMPLS_oSIMPLS)[-1,],
        type="l", xlab="component", ylab="equal digits", ylim=c(0,17),
        panel.first=grid())
legend("bottomleft", legend=c("PLS, SIMPLS", "PLS, OrthSIMPLS", "SIMPLS, OrthSIMPLS"),
       col=1:3, lty=1:3)
matplot(1:ncomp,cbind(cor_PLS_oSIMPLS,cor_SIMPLS_oSIMPLS,cor_SIMPLS_PLS), type="l",
        ylab="correlation", xlab="component", panel.first=grid())
legend("bottomleft", legend=c("PLS, SIMPLS", "PLS, OrthSIMPLS", "SIMPLS, OrthSIMPLS"),
       col=1:3, lty=1:3)

par(par.old)